Nicolas

L’histoire des cryptomonnaies (partie 1)

Partie II

Le BitGold

Le B-money à ouvert la porte au concept de cryptomonnaie. Quelques années plus tard, en 2005, Nick Szabo publie le concept de BitGold. Tandis que le B-money est un concept général de cryptomonnaie qui ne rentre pas dans le détail et qui se contente des grandes lignes, le BitGold détaille un peu plus le fonctionnement technique.  Contrairement au B-money qui voulait se passer du gouvernement, l’objectif du BitGold est de pouvoir se passer d’une entité tierce à qui l’on fait confiance pour gérer l’argent et sa valeur (gouvernement ou banque). Ainsi il veut éviter l’hyperinflation qui a pu avoir lieu avec des monnaies standards.

Nick Szabo

Un exemple de valeur d’échange qui ne dépends pas de tiers est les métaux précieux. Ceux-ci ont une valeur du fait de leur rareté et du coût d’extraction de ceux-ci mais il est trop coûteux de faire des analyses pour des transactions courantes. De ce fait bien que les métaux ne dépendent pas d’un tiers, un tiers de confiance entre en jeu afin de garantir la qualité d’un métaux. De plus il n’est pas facile de transporter ces métaux précieux et on ne peut payer sur internet avec.

Le but du BitGold est d’avoir un protocole où l’on pourrait créer des bits (un bit est un 0 ou un 1 sur un ordinateur, il faut prendre ça comme une pièce dans ce contexte) en ligne de manière très coûteuse (tout comme l’extraction des métaux précieux) avec très peu de dépendance à de tièrces parties. Le stockage et le transfère doivent aussi être facile. Le nom de BitGold vient de la compression du mot Bit (le bit informatique) et Gold (or en français).

Le fonctionnement

L’idée est de partir d’une chaine de bit, d’y appliquer une fonction (suite d’opérations pour transformer cette chaine) pour arriver à une autre chaine de bit constituant la preuve de travail. Les fonctions de hachage sont des fonctions qui prennent une chaine de caractère en entrée pour en sortir une autre. Si on prend une chaine et qu’on la prend en entrée, on aura toujours le même résultat en sortie. Une des particularités de ces fonctions est qu’elles ne sont pas reversibles : le seul moyen de trouver le texte d’origine est de tester toutes les possibilités jusqu’à constater que le résultat est le même une fois haché. Voici quelques exemples avec une fonction md5 :

coucou -> 721a9b52bfceacc503c056e3b9b93cfa

la blockchain c’est cool -> 3a90a467d43e64ce8a8399f796d8194d

Quelle que soit la longueur en entrée la longueur en sortie sera toujours de taille fixe. Si on modifie un caractère le résultat en sortie, appelé hash, ne sera plus le même. Ces fonctions sont des fonctions à un sens, on ne peut pas revenir en arrière : à partir d’un hash le seul moyen de retrouver la chaine en entrée est de tester toutes les possibilités et de la hacher jusqu’a retomber sur le même hash.

Les étapes pour la création de BitGold sont donc les suivantes :

• Une chaine de départ est créée
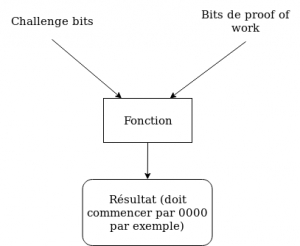
• Alice calcule sur son ordinateur la chaîne de Proof of Work. Il s’agit de la chaine de caractère qui une fois passée dans une fonction à un sens unique (une fois haché) avec la chaine de départ donne un résultat définit, par exemple une chaine qui commence par 2 zéros. Ce calcul est très coûteux car il faut tester beaucoup de possibilités jusqu’à tomber sur une chaîne de Proof of Work qui donne le résultat attendu (voir schéma).
• La chaîne de Proof of Work est horodatée de manière sécurisée par un serveur
• Alice ajoute la chaine de Proof of Work horodatée dans le registre (le fonctionnement du registre est détaillé ici)
• La chaine de départ correspond alors à la dernière chaîne ajoutée au BitGold (chaine de Proof of Work horodatée)
• Pour vérifier qu’Alice possède un BitGold en particulier, Bob doit regarder dans la chaine de titre contenue dans le registre de titre

Le contrôle d’Alice sur son BitGold dépend donc de sa dominance sur la chaine de titre dans le registre (dans le registre on peut voir qui possède le BitGold).

Afin de réguler la création de monnaie il convient de trouver une fonction ainsi qu’un résultat demandé qui soit assez difficile : plus c’est dur plus il faudra de temps pour créer de la monnaie. Il faut donc définir une difficulté mathématique. Cette difficulté peut être vérifiée dans le registre car les chaines sont horodatés (on peut regarder le nombre de pièces créées par jour par exemple). Ainsi si l’on créer une grosse quantité rapidement la valeur descend d’où l’interêt de la difficulté. Il est interessant de constater que l’auteur indique que les mineurs pourraient se rémunérer en revendant les pièces forgées sur les marchés et pourrait déployer des machines optimisés pour ces calculs, chose qui se fait actuellement avec les machines ASICS que l’on trouver pour miner le Bitcoin.

Le processus décrit ci-dessus est une première version de la blockhain (concept qui sera détaillé dans la prochaine partie) ainsi qu’une première version du système de minage. Le concept de Proof of Work est née.

L’auteur conclue en indiquant que ce protocole permet de résoudre des problèmes des monnaies fiduciaires telles que la contrefaçon. Cependant il reste le problème des fonds de départ qui sont cachés : si un créateur met en circulation 6000 BitGold mais qu’il en a gardé caché à la création 20 000 cela pose un problème qui devra être résolu par les futurs créateurs de ces monnaies.

Sources :

• Bit Gold, Nick Szabo (2005) – https://nakamotoinstitute.org/bit-gold/
• Secure Property Title with ower authority, Nick Szabo (1998à – https://nakamotoinstitute.org/secure-property-titles/

Partie I

Le commencement

Avant de parler du fonctionnement des cryptomonnaies voyons d’où cela vient.

Actuellement la plupart d’entre nous connaissent le Bitcoin. Le Bitcoin est la toute première des cryptomonnaies. Celle-ci a été inventée en 2008 : à cette date un certain Satoshi Nakamoto publie un document décrivant un système d’argent virtuel en P2P (peer to peer, de personne à personne) sur le site bitcoin.org. Cependant le Bitcoin n’existe pas vraiment, il ne s’agit là que d’un papier détaillant son fonctionnement.

Avant même les années 2000 le concept de cryptomonnaie commence petit à petit à se développer. David Chaum, un cryptographe américain, publie un document intitulé Untracable electronic cash, qui aborde le concept de monnaie électronique (le document date de 1990). Dans son article, il détaille le fonctionnement technique s’appuyant sur des techniques de cryptographie pour remplacer la monnaie physique (billets et pièces). Pour ce faire il faut que cette monnaie soit, comme la monnaie physique, infalsifiable et impossible à utiliser deux fois (on ne peut pas utiliser un même billet dans deux boutiques différentes, il faut le donner à une seule boutique).

Le Bitcoin n’invente donc pas tout les concepts, il se base sur différents papiers qui ont été publiés précédemment. Le document détaillant le principe du Bitcoin s’appuie notamment sur le concept de B-money inventé par Wei Dai en 1998.

B-Money

Wei Dai est intéressé par le concept de crypto-anarchie développé par Tim May. Le but de ces communautés est d’exclure le gouvernement car celui-ci ne serait pas nécessaire. Cependant aucun mode de fonctionnement n’était proposé pour qu’une communauté fonctionne sans avoir de gouvernement. Daprès Wei Dai une communauté est définie par une coopération de plusieurs personnes, ces échanges entre plusieurs personnes se basent sur un moyen d’échange : une monnaie. La monnaie étant traditionnellement mise en place et gérée par un gouvernement l’auteur propose deux systèmes (ou protocoles) pour s’en passer. Son papier propose une approche théorique pour avoir une monnaie décentralisée : il n’y a pas une entité qui s’occupe de gérer la monnaie, tout le monde y participe. Pour les deux protocoles Wei Dai suppose l’existence d’un réseau intraçable où les personnes sont identifiés par un identifiant (un numéro, clé publique) et les messages sont signés par l’expéditeur puis chiffrés. Maintenant que les pré-requis, ont été définis, voyons le fonctionnement.

Le premier protocole propose que chaque participant ait une base de données (ou livre de compte) où est enregistrée l’argent que chaque identifiant possède (tout le monde peut voir l’argent pour chaque identifiant mais ne sait pas à qui appartient l’identifiant). Pour le premier protocole on suppose un canal de communication synchrone, anonyme où les messages ne peuvent être perdus. Cela signifie que quand un message A est envoyé puis un message B, tous les destinataires reçoivent le message A avant le message B. L’auteur reconnaît que ça n’est pas faisable du fait de la contrainte d’avoir un canal de communication synchrone (Internet n’est pas un canal de communication synchrone par exemple) entre tous les participants.

• La création de la monnaie est ouverte à tous. Pour ce faire il suffirait de résoudre un problème calculatoire non résolu jusqu’à présent ou le résultat n’a aucune valeur et la durée nécessaire au calcul peut être déterminée. Ainsi la rémunération pour ce calcul se ferait par la création de monnaie en rapport avec le temps passé. Si on estime que 3 heures de travail valent 1 jeton, on peut proposer un problème calculatoire à résoudre qui prendra 3 heures et il sera rémunéré 3 jetons. Différentes autres méthodes de création sont suggérées à la fin de l’article.
• Pour transférer de l’argent il suffirait d’envoyer un message « Identifiant_A envoie X à Identifiant_B » le tout signé par Identifiant_A. Cette transaction est envoyé et enregistré par tout le monde sauf si Identifiant_A se retrouve avec un solde négatif.
• Le protocole prévoit aussi la création de contrats.

Le deuxième protocole est similaire au premier, cependant tout le monde ne possède pas la base de données, seulement quelques participants la possède. Les participants possédant la base de données sont appelés serveurs. Le premier protocole motive le deuxième de part son impraticabilité due aux contraintes sur les canaux de communication. Cette contrainte est levée pour ce protocole. Avec ce protocole seulement une partie des participants possèdent la base de données. Les serveurs sont reliés entre eux à l’aide d’un réseau Usenet. Usenet est un réseau inventé en 1979, servant principalement pour les forums. Un utilisateur peut se connecter à n’importe quel serveur. Lorsqu’une modification est faite sur un serveur cette modification est propagée aux autres serveurs et est ensuite disponible sur les autres serveurs.

Le fonctionnement est le même qu’auparavant, seulement lorsqu’un utilisateur effectue une transaction il doit vérifier que celle-ci a bien été reçue et traitée par un certain nombre de serveurs (choix aléatoire de serveurs).

L’idée est que chaque serveur possédant la donnée dépose une somme leur appartenant sur un compte spécial. Ce compte est utilisé pour récompenser ou infliger une amende au serveur en cas de preuve de mauvaise conduite (altération de la base de données pour frauder par exemple). Cette somme permet de s’assurer que les serveurs restent honnête et de les sanctionner si ce n’est pas le cas. Régulièrement les serveurs publient leurs bases de données. Chaque participant peut ainsi vérifier que la somme des montants des comptes ne soit pas supérieure à la somme totale d’argent en circulation pour éviter une expansion de la masse monétaire (duplication de l’argent). Si un nouveau serveur est créé il peut utiliser ce mécanisme pour se synchroniser avec les existants.

L’auteur conclue en précisant que le protocole peut sûrement être plus efficace et plus sûr. Il espère qu’avec cet article cela rends possible la « crypto-anarchie », ce que sera en effet le cas quelques années plus tard avec l’apparition du bitcoin, sujet que nous aborderons dans la prochaine partie.

Et la suite de l’histoire des cryptomonnaies, c’est par ici ! L’histoire des cryptomonnaies (partie 2).

Sources :

• Bitcoin: A Peer-to-Peer Electronic Cash System, Satoshi Nakamoto (2008) – https://bitcoin.org/bitcoin.pdf
• B-Money, Wei Dai (1998) – http://www.weidai.com/bmoney.txt